Collections and Control Flow

A collection is a kind of container that can hold zero or more objects. In this chapter, we illustrate several useful built-in collections including strings, lists, vectors, arrays, and tables.

In Dylan, a collection is an instance of the built-in class <collection>. Dylan provides a rich set of collection classes, and a rich set of generic functions to iterate over and to manipulate instances of those classes. In addition to using the built-in collection classes, you can define new collection classes. We present an example of defining a new collection class in Definition of a New Collection.

Control-flow functions enable you to alter the default (sequential) order of statement execution, including performing iteration. Dylan provides several ways of branching to different code depending on the value of one or more tests, as well as iterating over ranges of numbers and elements of collections.

In this chapter, we present collections and control flow together, because often Dylan control-flow constructs are used to operate on collections.

Built-in collection classes

Built-in collection classes. shows the most common Dylan collection classes.

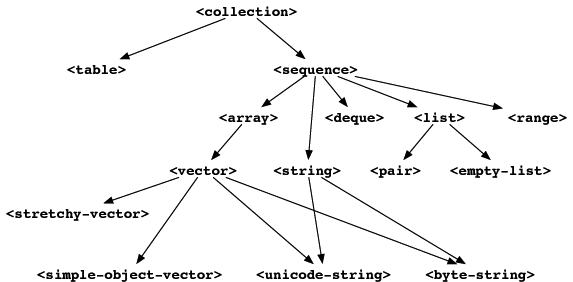
Built-in collection classes.

A collection holds a group of objects, called elements. Each element is associated with a key. Each class of collection can have different restrictions on keys or elements.

Sequences are an important subclass of collections. Sequences restrict their keys to be nonnegative integers starting at 0, and increasing by one for each additional value in the collection. Arrays, vectors, strings, and lists are sequences. Instances of <string> are sequences that can hold only characters. You can access instances of <array> using several subscripts. Instances of <vector> are one-dimensional arrays. Instances of <simple-object-vector> can hold any kind of Dylan object. Instances of most subclasses of <vector> cannot change size; the exception is instances of <stretchy-vector>.

Basic use of collections

In Sections Creation of strings and access to elements through Creation of lists and access to elements, we show how to create collections, and how to access the elements of a collection.

Creation of strings and access to elements

First, we define a variable, initializing it with a string:

? define variable *greeting* = "Hello, world.";

? *greeting*;
=> "Hello, world."

We can access elements of the string:

? *greeting*[0];
=> ’H’

? *greeting*[1];
=> ’e’

The syntax *greeting*[n] refers to the n th element of the string in *greeting*. You can use this syntax to access any element of any collection. In Dylan, double quotes are used to enclose literal strings, and single quotes are used to enclose characters.

We can use the assignment operator to change an element of a string:

? *greeting* := copy-sequence(*greeting*);
=>"Hello, world."

? *greeting*[0] := 'j';
=> ’j’

? *greeting*;
=> "jello, world."

We copied the greeting before modifying it, because modifying a literal constant is an error. A literal constant is an object whose contents are known completely at compile time. Dylan has a special syntax for each class of literal constant, so that they can be identified easily. The literal constant "Hello, world.", which is used to initialize the *greeting* variable, is part of the program executable, and is allocated when you compile the program.

The copy-sequence generic function returns a new collection with the same elements as its argument. The copy-sequence function creates the copy at run time, so modification of its results is permitted, because such changes do not alter the program itself. Note that, although the listener presents all objects in literal-constant syntax, not everything displayed by the listener is a literal constant.

The square-bracket syntax is an abbreviation for calling the generic function element. The following examples are equivalent:

? *greeting*[0];
=> ’j’

? element(*greeting*, 0);
=> ’j’

You can use either the square-bracket syntax or the element generic function on any collection. You must be careful if you use element as a local variable, however, because doing so will interfere with its use as a generic function, including the use of the square-bracket abbreviation.

Creation of vectors and access to elements

There are several ways to create collections. One way is to create a collection by using make. For example, here we create a vector that contains two elements:

? define variable *my-vector* = make(<vector>, size: 2);

We can change the first and second elements:

? *my-vector*[0] := 5;
=> 5

? *my-vector*[1] := 3;
=> 3

? *my-vector*;
=> #[5, 3]

If you want to create a sequence of a certain size, with every element having the same value, you can specify a fill keyword argument to make. The default value for the fill keyword parameter is #f. Thus, if you had read an element of *my-vector* before you wrote numbers into it, you would have received #f.

We can create and initialize a vector to different values all at once by using a built-in constructor. A constructor is a function that creates an instance; using it is a shorthand for calling make. Here, we use the vector constructor function to create a vector and to initialize it with data.

? define variable *my-vector* = vector(5, 3);

? *my-vector*;
=> #[5, 3]

As we saw in Creation of strings and access to elements, certain collections have a literal syntax that enables you to specify a particular data structure as part of the program:

? define variable *my-vector* = #[5, 3];

? *my-vector*;
=> #[5, 3]

Diagram of the vector #[5, 3]. shows how you can picture the vector that we just created.

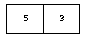
Diagram of the vector #[5, 3].

You might think that *my-vector* is a direct instance of <vector>, but it is not: The <vector> class is abstract, but instantiable. When you use the vector function, or use make with <vector>, the result is a general instance of <simple-object-vector>. You specify the size of a <simple-object-vector> when you create one, and you cannot change that size later. If you need a vector that can change size, use the <stretchy-vector> class. See A new collection class, for an example that uses stretchy vectors.

Creation of lists and access to elements

Lists are similar in purpose to vectors: Each one can store an ordered sequence of objects. Lists differ from vectors in that it is easy to add and remove elements from lists, especially at the front. In general, if the number of elements in a sequence will remain constant, lists are less efficient than vectors are.

Each element of a list is stored in a pair. A pair has two parts — a head and a tail. Typically, the head of a pair refers to an element, and the tail refers to the pair that holds the next element of the list. Normally, the final tail of the list is the empty list, represented by #(). Elements of lists can be any kind of object, including, of course, lists.

The list constructor function creates a list whose elements are the arguments provided:

? list(4, 5, 6);
=> #(4, 5, 6)

Diagram of the list #(4, 5, 6). is a diagram of the list that we just created.

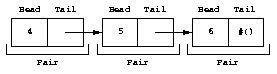
Diagram of the list #(4, 5, 6).

We can create a similar list by using the pair function, which creates one pair of the list at a time:

? pair(4, pair(5, pair(6, #())));
=> #(4, 5, 6)

As you can see, using list instead of pair, in this case, is much clearer. Note that Dylan provides functions called head and tail, which operate on lists:

? head(#(4, 5, 6));
=> 4

? tail(#(4, 5, 6));
=> #(5, 6)

? tail(tail(#(4, 5, 6)));
=> #(6)

A reference to the first pair of a list is exactly the same as a reference to the entire list.

We use head and tail when we define a method for copying lists in Lists and efficiency. We use pair in a method that copies lists recursively in A recursive list copier.

Iteration over a sequence

In the examples in Sections Building our own copy-sequence through Changes to a generic function’s signature, we show how to process each element of a sequence using different techniques.

Building our own copy-sequence

How would we write our own copy-sequence function, if Dylan did not already provide one? There are many possible approaches. One way would be to use a while loop. A while loop has a test expression (surrounded by parentheses) and a body. As long as the value of the test expression is true, the body will be executed repeatedly.

define method my-copy-sequence
    (old-sequence :: <sequence>) => (new-sequence :: <sequence>)
  let seq-size = old-sequence.size;
  let new-sequence = make(type-for-copy(old-sequence), size: seq-size);
  let index = 0;
  while (index < seq-size)
    new-sequence[index] := old-sequence[index];
    index := index + 1;
  end while;
  new-sequence;
end method my-copy-sequence;

The method my-copy-sequence makes a new sequence of the same size as its argument, then iterates over all the elements of the argument, storing each element of the sequence into the appropriate element of the new sequence. The size generic function returns the number of elements in a collection. In this example, the while loop terminates when index reaches the size of the sequence.

The type-for-copy generic function returns an appropriate class for make, given an object that you wish to copy. For most collections, type-for-copy just returns the class of the collection provided.

Iteration with for

We can use the for to express concisely a loop that increments a variable until a limit is reached.

define method my-copy-sequence
    (old-sequence :: <sequence>) => (new-sequence :: <sequence>)
  let new-sequence
    = make(type-for-copy(old-sequence), size: old-sequence.size);
  for (index from 0 below old-sequence.size)
    new-sequence[index] := old-sequence[index];
  end for;
  new-sequence;
end method my-copy-sequence;

In the preceding example, the body is executed old-sequence.size times, with index bound to zero first, then rebound to one more than the previous value of index each time through the loop. The variable index is defined only within the body of the for iteration construct. The body of the for iteration construct begins after the iteration clause(s), and finishes with the matching end. For the while iteration construct shown in Building our own copy-sequence, the body starts after the predicate and finishes with the matching end.

The for loop can have many different kinds of iteration clauses. In this section, we have shown a simple iteration over a series of numbers. In Lists and efficiency, we use clauses that bind variables to initial values for the first time through a loop, and use expressions to rebind the variables for the second and subsequent times through the loop. We also demonstrate a clause that permits iteration to continue until an expression is true, both in Lists and efficiency and Adding and removing elements.

The for loop has a simple type of iteration clause that we can use to iterate over any Dylan collection. The airport example in Vehicle containers, demonstrates iteration over vectors using this kind of iteration clause.

Lists and efficiency

The my-copy-sequence method in Iteration with for works efficiently for vectors. It does so because Dylan can store and retrieve arbitrary elements of vectors, and can determine the size of vectors in constant time.

Lists are quite a different data structure from vectors. Accessing elements and determining the size of a list takes linear time. Thus, you can access the thousandth element of a vector or string in the same amount of time as you can access the first element of a vector or string; when you uses lists, however, it takes about 1000 times longer to access the thousandth element than to access the first element. The difference in access times occurs because Dylan must walk over almost 1000 pairs to get to the thousandth pair, and thus get to the thousandth element of the list. Although the method defined in Iteration with for can copy lists, it will be excessively slow, especially for long lists.

We would like to provide a special method for copying lists that uses a more efficient algorithm. In particular, we want to walk over the provided list element by element, without having to retrace over elements of the list that we have already copied.

// Assumes that old-list is a proper list (that is, it ends with #())
// and is not circular
define method my-copy-sequence (old-list :: <list>) => (new-list :: <list>)
  let new-list = make(<list>, size: old-list.size);
  for (old = old-list then old.tail,
       new = new-list then new.tail,
       until: empty?(old))
    new.head := old.head;
  end for;
  new-list;
end method my-copy-sequence;

First, my-copy-sequence makes a new list that is the same length as the old one. Next, the for iterator is used to bind the variables old and new to old-list and new-list, respectively. Then, the for iterator executes the until: expression to determine whether it is time to terminate the loop. If the until: expression returns true, then the for loop terminates, and the newly created list is returned from my-copy-sequence. Otherwise, the body of the for loop is executed — the body stores the head of the first pair in old into the head of the first pair in new. The result of that action is that the first element of new is identical to the first element of old. For this iteration, that action causes the first element of new-list to be identical to the first element of old-list. In subsequent iterations, the body will access elements 1 closer to the end of the list. It will do so because, after the body is executed, the for iterator loops back to the iterator clauses, where the then clauses bind old to all but the first pair of old, and bind new to all but the first pair of new. The termination check occurs again, with the same consequences, depending on the value of the until: expression. Iteration then continues just like the second time through the loop until the end of old is reached.

In this method, we never have to search for the current spot of the old list that we are copying, or to search for the end of the new list that we are building. The variables old and new track exactly which pairs in the iteration to access, and that tracking saves a considerable amount of time for large lists. When the iteration is finished, my-copy-sequence returns the new list.

Polymorphism

An important advantage of programming in Dylan is that we can provide a general method for copying a sequence (as shown in Iteration with for), and also can provide special copying methods for particular subclasses of sequences (as shown in Lists and efficiency). Method dispatch takes care of picking the best method for the argument. Callers of my-copy-sequence do not need to worry about any performance optimizations that we have installed for lists. They simply use my-copy-sequence for lists, just as they would for any other sequence. This polymorphism can be useful for keeping interfaces between components of a program simple and extensible.

Mapping functions

Iterating over all the elements of a collection is a common idiom, and Dylan provides several different mapping functions that accomplish these kinds of iterations in different ways. In the following example, we redefine the my-copy-sequence method originally defined in Lists and efficiency. Here, we use the do iteration construct, instead of a for loop.

// Assumes that old-list is a proper list (that is, it ends with #())
// and is not circular
define method my-copy-sequence (old-list :: <list>) => (new-list :: <list>)
  let new-list = make(<list>, size: old-list.size);
  // Remember the pair of the copy that we are initializing
  let current-pair = new-list;
  // Iterate over all the elements of the existing list, making new pairs,
  // and splicing them into the end of the copy that we are building
  do(method (old-element)
       current-pair.head := old-element;
       current-pair := current-pair.tail;
     end method,
     old-list);
  new-list;
end method my-copy-sequence;

The do mapping function takes a function and one or more collections, and calls the function on each element of each collection. The function should take one argument if you provide do with one collection, two arguments if you provide two collections, and so on. The result of calling the function is ignored, and do itself returns no meaningful value. The do function is useful only if the method that you provide accomplishes a valuable side effect. In the preceding example, the supplied method stores an element of the old list into the head of the current pair of the new list, and moves to the next pair of the new list. Note that this method is actually a closure, which closes over the current-pair local variable. See Closures, for more information about closures.

A recursive list copier

In many situations, the most concise way to manipulate lists (and other treelike structures) is to use recursion. In recursion, a function calls itself, directly or indirectly. In the following example, we redefine the my-copy-sequence method for lists to use recursion instead of iteration.

define method my-copy-sequence (old-list :: <list>) => (new-list :: <list>)
  if (empty?(old-list))
    #();
  else
    pair(old-list.head, my-copy-sequence(old-list.tail));
  end if;
end method my-copy-sequence;

Note that recursion can be just as efficient as iteration. For example, consider the function my-reverse, which creates a new list with elements in the reverse order from the list you supply.

define method my-reverse (old-list :: <list>) => (reversed-list :: <list>)
  local method rev (old :: <list>, results :: <list>)
    if (empty?(old)) results else rev(old.tail, pair(old.head, results)) end;
  end method;
  rev(old-list, #());
end method my-reverse;

The local method declaration inside the my-reverse method defines a function that is bound to the name rev only within a scope of the body of my-reverse. This declaration is different from define method, which creates module bindings that can be accessed outside the lexical scope of where they are defined.

The local method rev calls itself as the last expression in its body. Thus, the rev method can be optimized by the Dylan compiler into code that is exactly as efficient as if it was written with iteration.

Alternative ways of defining the my-reverse function are discussed in Reversal of sequences.

Using map and curry

Perhaps the easiest way to implement our simple sequence copier is to use the map function. The map function takes the same arguments as does do. However, instead of ignoring the return value of the function that you provide, map gathers into a new collection all the results of calling the provided function. The new collection will be an instance of the type-for-copy of the first collection argument to map.

define method my-copy-sequence
    (old-sequence :: <sequence>) => (new-sequence :: <sequence>)
  map(identity, old-sequence);
end method my-copy-sequence;

The identity function simply returns its argument without making any changes. A more interesting example is to define a method that multiplies a number by each element of a vector, yielding a new vector with the products. Here is a sample call to scalar-multiply, which we define next:

? scalar-multiply(3, #[4, 5, 6]);
=> #[12, 15, 18]

Here is our definition of scalar-multiply, using map:

define method scalar-multiply
    (scalar :: <number>, old-vector :: <vector>) => (result :: <vector>)
  map(method (vector-element) scalar * vector-element end,
      old-vector);
end method scalar-multiply;

We use the method statement to create a kind of function (a closure) that multiplies scalar by an element of the vector provided by map. The map iterator then calls that function on each element of old-vector, collecting the results in a new sequence. A variant of map, called map-into, replaces elements in an existing collection, rather than creating a new collection for the results. See Basic collection methods, for an example of the use of map-into.

We can define this method more succinctly using curry, which is a function that generates a function:

define method scalar-multiply
    (scalar :: <number>, old-vector :: <vector>) => (result :: <vector>)
  map(curry(\*, scalar), old-vector);
end method scalar-multiply;

The curry function in this example creates exactly the same method as the one that we created in the previous definition of scalar-multiply. That is, curry(\*, scalar) builds a function that multiplies its argument by scalar. This generated function is then used by map to compute the value of each element of the new sequence.

Mapping functions such as do and map work well when you want to operate over the entire collection. The map function works well only if there is a one-to-one correspondence between input-collection sizes and output-collection size. However, the other techniques that we have presented, such as using for and while, can work better when you want to operate on only part of a sequence. In A sequence copier that can copy a portion of a sequence, we take another look at how a for loop can help us to solve the problem of iterating over only part of a collection.

A sequence copier that can copy a portion of a sequence

The copy-sequence generic function provided by Dylan actually takes keyword arguments that allow only a portion of the sequence to be copied. Here is an example:

? copy-sequence("airport", start: 3);
=> "port"

? copy-sequence("snow", start: 1, end: 3);
=> "no"

In the following, we use a for loop with two iteration clauses to implement the more flexible version of the general purpose my-copy-sequence:

define method my-copy-sequence
    (old-sequence :: <sequence>,
     #key start = 0, end: limit = old-sequence.size)
 => (new-sequence :: <sequence>)
  let new-sequence = make(type-for-copy(old-sequence), size: limit - start);
  for (source-index from start below limit,
       destination-index from 0)
    new-sequence[destination-index] := old-sequence[source-index];
  end for;
  new-sequence;
end method my-copy-sequence;

In the preceding example, we force the keyword parameter end: to bind the variable limit, rather than binding end. It is illegal to use end as a variable name, because end is one of a few reserved words in Dylan. In the body of the for loop, source-index will range from start to 1 less than limit, and destination-index will range from 0 to 1 less then limit minus start, which is the length of the new sequence being created.

Changes to a generic function’s signature

Note that the my-copy-sequence method defined in A sequence copier that can copy a portion of a sequence has a parameter list that is not congruent with the parameter list of the generic function. That is, that method accepts the start: and end: keyword arguments, when previously only required arguments were allowed for that generic function. We did not explicitly define the my-copy-sequence generic function; Dylan created the generic function implicitly, when we defined the first method for it, in Building our own copy-sequence. The generic function accepts two required parameters, and no keyword parameters.

When you need to change the signature of a generic function, you must change all the methods for that generic function to have a compatible signature. In our example, we would have to fix the my-copy-sequence method for lists to accept the start: and end: keyword arguments, and would have to change the methods to operate on only a portion of the list provided. For more information about the congruence rules for methods of a generic function, see Parameter-list congruence.

Manipulation of collections

Dylan provides an extensive library of functions that manipulate collections. In this section, we explore how to build complex collection functions from simpler ones, using the control-flow functions already shown in this chapter.

Reversal of sequences

Dylan provides two generic functions for reversing sequences: reverse, and reverse!. They both achieve the same objective, but reverse! is allowed to modify its argument, whereas reverse never modifies its argument.

? reverse("lever");
=> "revel"

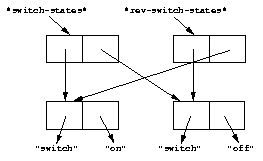
? define variable *switch* = vector("switch", "on");

? reverse(*switch*);
=> #["on", "switch"]

? *switch*;
=> #["switch", "on"]

? reverse!(*switch*);
=> #["on", "switch"]

After the call to reverse!, the value of *switch* is not defined. Only the return value from reverse! will be meaningful. If we want *switch* to contain the reversed sequence, we must instead write

? *switch* := reverse!(*switch*);
=> #["on", "switch"]

? *switch*;
=> #["on", "switch"]

Note that reverse! cannot change the object to which *switch* refers; however, reverse! is allowed to alter the contents of that object. Also note that reverse! may not return the same object as that you provide as its argument. Consider the case of using reverse! on a list to see how this behavior can be useful.

Convention:

Dylan has a convention of putting an exclamation point at the ends of the names of functions that can destructively modify their arguments. For example, reverse! takes a sequence, and returns a sequence that has the same elements but in reverse order. The reverse! generic function may change the sequence that is its argument. In contrast, the reverse generic function performs a similar operation, but does not destructively modify its argument. Setters are an exception to this convention: They modify their argument, but do not typically end with !.

How can we write our own version of reverse using the iteration techniques presented so far?

define method my-reverse (seq :: <sequence>) => (reversed-seq :: <sequence>)
  let reversed-seq = make(type-for-copy(seq), size: seq.size);
  for (destination-index from seq.size - 1 to 0 by -1,
       source-index from 0)
    reversed-seq[destination-index] := seq[source-index];
  end for;
  reversed-seq;
end method my-reverse;

Once again, this algorithm is fine for vectors and strings, but has poor performance for lists. Here is a special my-reverse method for lists:

define method my-reverse (old-list :: <list>) => (reversed-list :: <list>)
  let reversed-list = #();
  for (old-element in old-list)
    reversed-list := pair(old-element, reversed-list);
  end for;
  reversed-list;
end method my-reverse;

It is easy to build up a list from its end to its start, and that is exactly what we do in the preceding method. We start with the empty list, and add pairs to the reversed list whose heads are the elements of the argument. We follow the old list from its start to its end, while we build the new list from its end to its start, thus reversing the list.

It is important to remember that, even though we created a new sequence to contain the elements of the old sequence, we still share those old elements with the new sequence. If two elements of a collection refer to the same object, then modifying the element of one of the collections affects the value of the element of the other collection. We illustrate this behavior in Destructive operations and shared structure.

Destructive operations and shared structure

Consider the following example, and Figures State before the element is changed. and State after the element is changed..

// First we construct a vector of two vectors
? define variable *switch-states*
    = vector(vector("switch", "on"), vector("switch", "off"));

? *switch-states*;
=> #[#["switch", "on"], #["switch", "off"]]

// Now, we reverse the vector, holding on to the result
? define variable *rev-switch-states* =
    my-reverse(*switch-states*);

At this point, the states of the variables and vectors correspond to State before the element is changed..

We examine the two sequences:

? *rev-switch-states*;
=> #[#["switch", "off"], #["switch", "on"]]

  // Although *switch-states* and *rev-switch-states* are different vectors,
  // they share elements
? *switch-states* == *rev-switch-states*;
=> #f

State before the element is changed.

Now, we change an element:

? *switch-states*[0] == *rev-switch-states*[1];
=> #t

  // So, when we change an element in one, the same change occurs in the other
? (*switch-states*[0])[0] := "master switch";
=> "master switch"

At this point, the states of the variables and vectors correspond to State after the element is changed..

State after the element is changed.

We can look at the values of the variables:

? *switch-states*;
=> #[#["master switch", "on"], #["switch", "off"]]

? *rev-switch-states*;
=> #[#["switch", "off"], #["master switch", "on"]]

Each object pictured in Figures State before the element is changed. and State after the element is changed. is a vector. The strings in the figures are vectors, although we did not draw them as such, to keep the diagrams relatively simple. Variables are not objects in Dylan, but they are shown referring to objects. In State after the element is changed., the string "switch" is not referenced by any other object and is therefore garbage; eventually, it will be reclaimed by a garbage collector.

Changing an element of one collection can affect another collection if the two collections share elements. Two collections share an element if there is a value in one collection that is == (that is, identical) to a value in the other collection. Functions such as copy-sequence and reverse do only a shallow copy of their arguments: only the top level of the copy is new. Every other part is shared with the old sequence. Thus, it is important to take care when you modify objects that might be shared with other parts of your application. Using well-defined module boundaries that specify whether data structures can be modified by clients of the module can help you to keep application data consistent.

Conditional execution

In Sections if, else, and elseif through Search of arrays with find-key, we consider ways to execute different code depending on the results of one or more tests.

if, else, and elseif

We showed the simplest use of if in Methods on <time-offset>. Consider the case where there is more than one test involved. Suppose that we want to write a method that describes a vote. Here are sample calls to interpret-votes:

? interpret-votes(yes: 4, no: 0);
=> "unanimously approved"

? interpret-votes(yes: 3, no: 1);
=> "approved"

? interpret-votes(yes: 2, no: 2);
=> "tie"

? interpret-votes(yes: 1, no: 3);
=> "not approved"

We can define the interpret-votes method using the if control structure and the else clause:

define method interpret-votes
    (#key yes :: <nonnegative-integer> = 0, no :: <nonnegative-integer> = 0)
 => (interpretation :: <string>)
  if (yes > 0 & no = 0)
    "unanimously approved";
  else if (yes > no)
    "approved";
  else if (yes = no)
    "tie";
  else
    "not approved";
  end if;
  end if;
  end if;
end method interpret-votes;

We defined the <nonnegative-integer> type in Examples of types that are not classes, using limited. Only positive integers and the integer 0 are instances of <nonnegative-integer>. We use this type in the interpret-votes method parameter list to ensure that no negative vote counts are accepted.

Quick summary of & infix operator : arg1 & arg2

The infix operator & does the and logical operation. If either or both of the arguments to the & operator are false, then & returns false.

Note that the & operator is actually a control-flow operator. If the first argument to the & operator is false, then the value of the second argument is never computed, and false is returned. If the value of the first argument is true, then the value of the second argument is computed and returned.

The | operator (logical or) behaves in a similar manner, except that its second argument is computed and returned only if the first argument is false.

The syntax for the if control structure allows elseif clauses, which makes this style of conditionalization slightly more compact:

define method interpret-votes
    (#key yes :: <nonnegative-integer> = 0, no :: <nonnegative-integer> = 0)
 => (interpretation :: <string>)
  if (yes > 0 & no = 0)
    "unanimously approved";
  elseif (yes > no)
    "approved";
  elseif (yes = no)
    "tie";
  else
    "not approved";
  end if;
end method interpret-votes;

Branching with case

Dylan also provides the case control structure to give you an alternative way to express the branching style shown in if, else, and elseif:

define method interpret-votes
   (#key yes :: <nonnegative-integer> = 0, no :: <nonnegative-integer> = 0)
 => (interpretation :: <string>)
  case (yes > 0 & no = 0) => "unanimously approved";
       (yes > no) => "approved";
       (yes = no) => "tie";
       otherwise => "not approved";
  end case;
end method interpret-votes;

The decision of whether to use if with elseif and else as opposed to using case, is largely a matter of personal style.

Branching with select

In certain situations, you are working with a particular two-argument predicate (such as == or <). The value of the first argument to the predicate will always be the same, and you would like to perform different actions based on the second value. You can use both if and case to handle this situation, but the select control structure is more concise. The following example interprets traffic-light colors:

define method color-action
    (color :: <symbol>) => (action :: <symbol>)
  select (color)
    #"red" => #"stop";
    #"yellow" => #"slow";
    #"green" => #"go";
  end select;
end method color-action;

The select control structure uses == for the default predicate. For example, in the preceding select statement, the symbol #"stop" will be returned if color == #"red". If you require a different predicate, use the by clause, as shown in the following example, which interprets age from a number representing years:

define method interpret-age
    (age :: <nonnegative-integer>) => (description :: <string>)
  select (age by \<)
    13 => "youngster";
    20 => "teenager";
    60 => "adult";
    otherwise => "senior";
  end select;
end method interpret-age;

The preceding method returns the string "youngster" when provided an age less then 13; returns "teenager" when the age is between 13 and 20; and returns "adult" when the age is between 20 and 60. In all other cases, it returns "senior".

Tables: Dynamic associations

In Branching with select, we saw how the color-action method associated traffic-light colors with actions by using select. These associations are static. They are determined at compile time, and you cannot change them without recompiling the color-action method. Sometimes, it is useful to associate one object with another dynamically, while the program is running. Collections are good data structures for this purpose. How could we rewrite color-action so that it uses a collection to associate colors with actions?

define variable *color-action-table* = make(<table>, size: 3);

*color-action-table*[#"red"] := #"stop";
*color-action-table*[#"yellow"] := #"slow";
*color-action-table*[#"green"] := #"go";

define method color-action (color :: <symbol>) => (action :: <symbol>)
    *color-action-table*[color];
end method color-action;

The tables provided by Dylan use == to compare keys.

During the execution of the program, we could add new associations to *color-action-table*, or could change or remove existing associations. Tables grow as necessary to accommodate new associations that are added.

Search of arrays with for and block

Suppose that you wanted to search a two-dimensional array, and to return the first number greater than a given value.

define method find-larger-than
    (2d-array :: <array>, value :: <integer>)
 => (result :: type-union(singleton(#f), <integer>))
  let first-dimension = dimension(2d-array, 0);
  let second-dimension = dimension(2d-array, 1);
  block (return)
    for (i from 0 below first-dimension)
      for (j from 0 below second-dimension)
        if (2d-array[i, j] > value)
          return(2d-array[i, j]);
        end if;
      end for;
    end for;
    #f;
  end block;
end method find-larger-than;

In the preceding example, the block statement binds the variable return to a nonlocal exit procedure. If this exit procedure is called while the block is in effect, it will return immediately from the block statement, using any provided arguments as return values. Thus, if an element of 2d-array is greater than value, then this element will be returned immediately from the block, and thus from the method. Array elements can be accessed with the square-bracket syntax, or with the function aref. (For more information about referencing elements of an array, see Element references.) If the entire array is searched, and no element is found that is greater than value, then the for loops exit normally and the block statement returns the last value in the block body, which in this case is false. We use the type-union type-generating function to create a type that permits either false or an integer to be returned from this method.

Search of arrays with find-key

In Dylan, we can access multidimensional arrays as though they are linearized one-dimensional vectors by using the element generic function. Dylan provides a find-key generic function that uses element to find the index (or key) that corresponds to a desired value in a collection. Here, we rewrite find-larger-than to use find-key :

define method find-larger-than
    (array :: <array>, value :: <integer>)
 => (result :: type-union(singleton(#f), <integer>))
  let index
    = find-key(array, method (array-element) array-element > value end);
  index & array[index];
end method find-larger-than;

The find-key generic function searches an array, calling the function that we provided on each element. If our function ever returns true, find-key returns the linearized index of the array element containing the value. For a two-dimensional array, the linearized index is the index that would be the appropriate key of a one-dimensional array that we could construct by placing the rows of the two-dimensional array one after the other. Rows in a two-dimensional array are numbered with the first subscript, and the column within those rows is numbered by the second subscript.

If our function never returns true for any element, find-key returns false. In this example & is truly used as a control structure. If index is false, then & will return false without executing the array access. If index is true, then the array access occurs, and that is the value of the & expression, and thus the value returned from the method.

Summary

In this chapter, we covered the following:

• We showed a selection of built-in collection classes, including strings, lists, vectors, tables, and arrays.

• We showed various iteration facilities and control structures, including for, do, map, while, if, case, select, block, &, and |.

• We showed a simple example of recursion.

• We showed some basic collection functions: element, size, and find-key.

• We showed some basic sequence functions: copy-sequence, and reverse.

• We showed additional collection functions: head, tail, pair, list, and vector.

• We explored basic sequence algorithms, and found that, although the various sequence classes are related, algorithms that are efficient for one class of sequence may not be appropriate for a different class of sequence.

• We discussed destructive versus nondestructive functions.

• We demonstrated the curry function, which generates functions.

• We showed several examples of the use of closures as arguments to iterators.